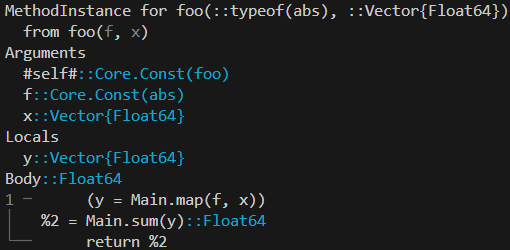
Generic expressions are represented by <something> (e.g., <function> or <operator>). This is just notation, and the symbols < and > should not be misconstrued as Julia's syntax.
If you want to adjust the size of the font, zoom in or out on pages by respectively using Ctrl++ and Ctrl+-. The layout will adjust automatically.
To quickly share a link to a specific section, simply hover over the title and click on it. The link will be automatically copied to your clipboard, ready to be pasted.
| Action | Keyboard Shortcut |
|---|
| Previous Section | Ctrl + 🠘 |
| Next Section | Ctrl + 🠚 |
| List of Subsections | Ctrl + x |
| Close Any Popped Up Window (like this one) | Esc |
| Open All Codes and Outputs in a Post | Alt + 🠛 |
| Close All Codes and Outputs in a Post | Alt + 🠙 |
When benchmarking, the equivalence of time measures is as follows.
| Unit | Acronym | Measure in Seconds |
|---|
| Seconds | s | 1 |
| Milliseconds | ms | 10-3 |
| Microseconds | μs | 10-6 |
| Nanoseconds | ns | 10-9 |
 Home
Home Chapters
Chapters Links
Links BOOK in PDF
BOOK in PDF