pic
Personal
Website

8b. Defining Type Stability

Martin Alfaro
PhD in Economics
Code Script
This section's scripts are available here, under the name allCode.jl. They've been tested under Julia 1.11.3.

Introduction

One of the primary reasons Julia achieves high performance is its ability to generate specialized machine code adapted to specific argument types. This capability relies heavily on type inference, the process by which the compiler deduces the types of variables and intermediate results before execution. When the compiler can successfully predict the concrete types of all operations within a function body, the resulting code is described as type stable.

Type stability isn't merely a theoretical ideal, but rather a practical requirement for writing efficient Julia programs. Without it, the compiler is forced to generate generic code, leading to significant performance penalties.

This section formally defines type stability and reviews the tools employed for its verification. In the next section, we'll start to examine how type stability applies in specific scenarios.

An Intuition

When a function is called, Julia follows a well‑defined sequence of steps to determine how that call should be executed. We previously described this process. To briefly review it, consider a function foo(x) = x + 2 and the execution of foo(a) for some variable a. We assume a has a specific value assigned and therefore a concrete type, although we omit explicitly specifying a value for a. This lets us highlight that the process unfolded depends on types, rather than values.

When evaluating foo(a), Julia first determines the concrete type of a, which we'll denote as T. It then checks whether a compiled method instance of foo specialized for an argument of type T already exists. If such an instance exists, then foo(a) is executed immediately. Otherwise, Julia proceeds to compile one. This compilation step lverages type inference, wherein the compiler attempts to deduce concrete types for all terms within the function body. The resulting machine code is then stored, making it readily available for subsequent calls of foo(b) with b having type T.

Type Stability and Performance

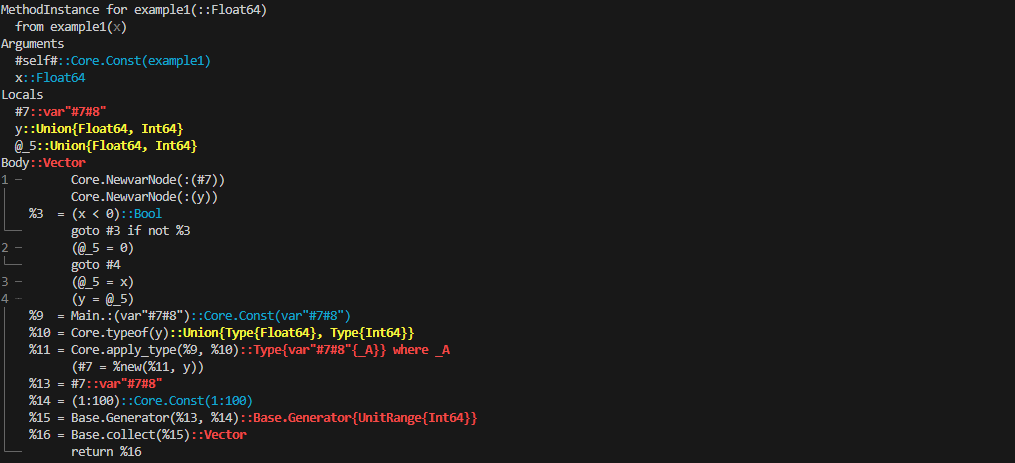
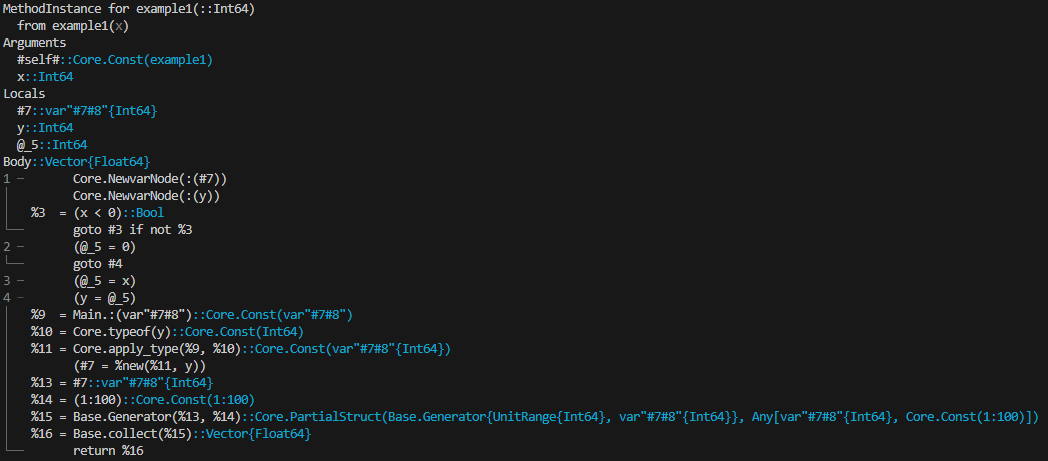
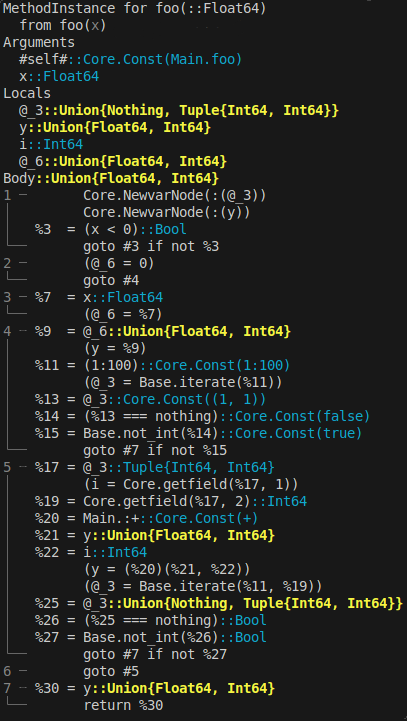
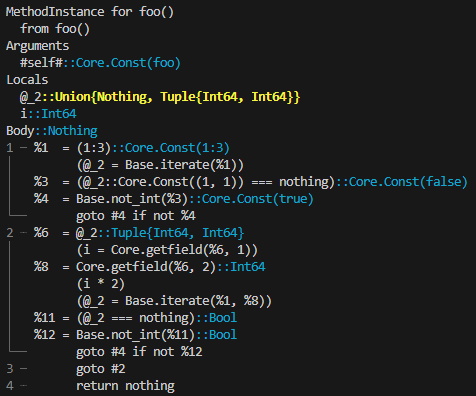
The key to generating fast code lies in the information available to the compiler during the compilation stage. This information is primarily gathered through type inference, where the compiler identifies the specific type of each variable and expression involved. When the compiler can accurately predict a single concrete type for the function's output, the function call is said to be type stable.

While this constitutes the formal definition of type stability, a more stringent definition is usually applied in practice: the compiler must be able to infer concrete types for each expression within the function, not only for the final output. This definition aligns with the output provided by @code_warntype. This is the built-in macro to detect type instabilities, which we'll present in the next subsection.

When type stability holds, the compiler can specialize the computational approach for each operation, resulting in fast execution. Essentially, type stability dictates that there's sufficient information to determine a straight execution path, thus avoiding unnecessary type checks and dispatches at runtime.

In contrast, type-unstable functions generate generic code, thus accommodating each possible combination of concrete types. This results in additional overhead during runtime, where Julia is forced to dynamically gather type information and perform extra calculations based on it. The consequence is a pronounced deterioration in performance.

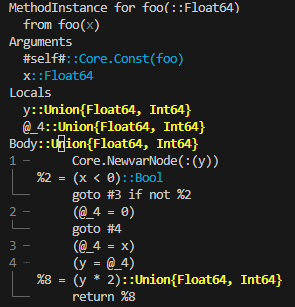
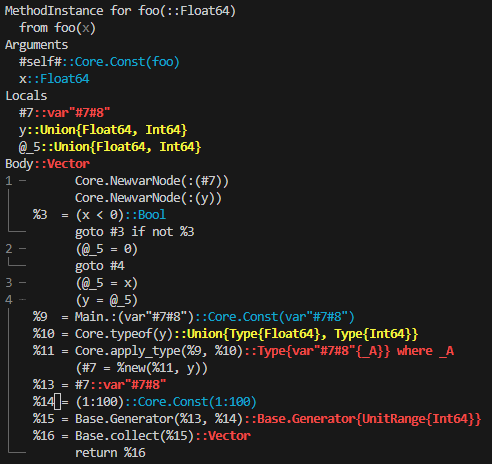
Type Stability Characterizes Function Calls
It's common to describe a function as "type stable". Strictly speaking, however, type stability isn't a property of the function. Rather, it's a property of how the function behaves when called with arguments of particular concrete types. The distinction is crucial in practice, since a function may exhibit type stability for certain input types, but not for others.

An Example

To identify type stability in practice, let's consider the following example.

x = [1, 2, 3]                  # `x` has type `Vector{Int64}`

@ctime sum($x[1:2])            # type stable
Output in REPL
  12.598 ns (2 allocations: 80 bytes)

x = [1, 2, "hello"]            # `x` has type `Vector{Any}`

@ctime sum($x[1:2])            # type UNSTABLE
Output in REPL
  23.696 ns (2 allocations: 80 bytes)

The two operations may look identical at first glance, since both ultimately evaluate 1 + 2. However, the way Julia compiles and executes each version differs significantly, and the first approach ends up being faster. The key distinction is that the first function is type stable.

In that first version, the expression x[1] + x[2] can be inferred to have type Int64. Because the compiler can determine that both x[1] and x[2] are Int64, it’s able to generate efficient, specialized machine code for this concrete type. Importantly, this optimization isn’t limited to the specific example shown: any call of the form sum(y) where y is a Vector{Int64} benefits from the same specialization.

The second version, however, introduces type instability. Here, x has type Vector{Any}, which prevents the compiler from deducing a single concrete type for the expression x[1] + x[2]. Since the elements of a Vector{Any} may hold values of any subtype of Any, the compiler can’t predict whether x[1] or x[2] will be an Int64, a Float64, a Float32, or other type. This results in slow compiled code, and the penalty applies to every call of sum(y) where y is a Vector{Any}.

Remark
Julia's developers are continually refining the compiler, addressing and mitigating the effects of certain type instabilities. As a result, many operations that were once type unstable are now type stable. This means that type stability should be considered a dynamic property of the language, subject to change as the compiler evolves.

Checking for Type Stability

There are several mechanisms to determine whether a function call is type stable. One of them is based on the @code_warntype macro, which reports all the types inferred during a function call. To illustrate its use, consider a function that defines y as a transformation of x, and then uses y to perform some operation.

function foo(x)
    y = (x < 0) ?  0  :  x
    
    return [y * i for i in 1:100]
end
Output in REPL
julia>
@code_warntype foo(1.0)

function foo(x)
    y = (x < 0) ?  0  :  x
    
    return [y * i for i in 1:100]
end
Output in REPL
julia>
@code_warntype foo(1)

The output of @code_warntype can be difficult to interpret. Nonetheless, the inclusion of colors facilitates its understanding:

  • If all lines are blue, the function is type stable. This means that Julia can identify a unique concrete type for each expression.

  • If at least one line is red, the function is type unstable. It reflects that one expression or more could potentially adopt multiple possible types.

  • Yellow lines indicate type instabilities that the compiler can handle effectively (in the sense that they have a reduced impact on performance). As a rule of thumb, you can safely ignore them.

Warning!
Throughout the website, we'll refer to type instabilities as those indicated by a red warning exclusively. Yellow warnings will be mostly ignored.

In the provided example, the compiler attempts to infer concrete types. This is done by identifying two pieces of information, given x's concrete type:

  1. the type of y,

  2. the type of y * i where i has type Int64, implicitly defining the type of [y * i for i in 1:100].

The example clearly demonstrates that the same function can be type stable or unstable depending on the types of its inputs: foo is type stable when x has type Int64, but type unstable when x is Float64.

Specifically, in the scenario where x = 1, the compiler infers for i) that y can be equal to either 0 or x. Since both 0 and 1 are Int64, the compiler identifies a unique type for y, given by Int64. Regarding ii), y * i also yields an Int64, as both i and y have type Int64. This determines that [y * i for i in 1:100] has type Vector{Int64}. Consequently, foo(1) is type stable, enabling Julia to invoke a method specialized for integers.

As for x = 1.0, the information for i) is that y could be either 0 or 1.0. As a result, the compiler can't infer a unique type for y, which could be either Int64 or Float64. The @code_warntype macro reflects this, identifying y as having type Union{Float64, Int64}. This ambiguity affects ii), forcing the compiler to consider approaches that handle both Float64 and Int64, and hence preventing specialization. Overall, foo(1.0) is type unstable, which has a detrimental impact on performance.

Function Call Leverage Information on Types, Not Values
The conclusions regarding type stability wouldn't have changed if we had considered foo(-2) or foo(-2.0) in each tab, respectively. Type stability depends on whether x has type Int64 or Float64, regardless of its actual value. Since the compiler analyzes type information exclusively, the actual numeric value plays no role in determining type stability.

Yellow Warnings May Turn Red

Not all type instabilities carry the same performance cost, and Julia indicates their severity through yellow and red warnings. A yellow warning typically signals a mild issue: the compiler has detected a type instability, but it occurs in a small isolated computation that Julia can still optimize reasonably well. However, repeated execution of these operations may escalate into more serious performance issues, triggering a red warning. The following example demonstrates a scenario like this.

function foo(x)
    y = (x < 0) ?  0  :  x
    
    y * 2
end
Output in REPL
julia>
@code_warntype foo(1.0)

function foo(x)
    y = (x < 0) ?  0  :  x
    
    [y * i for i in 1:100]
end
Output in REPL
julia>
@code_warntype foo(1.0)

function foo(x)
    y = (x < 0) ?  0  :  x    
    
    for i in 1:100
      y = y + i
    end
    
    return y
end
Output in REPL
julia>
@code_warntype foo(1.0)

In the first case, the yellow warning appears because the expression y * 2 may produce either a Float64 or an Int64. Since this computation happens only once and involves types the compiler can handle efficiently, the impact on performance is minimal. In contrast, the second tab performs repeated evaluations of y * i without a stable concrete type for y, resulting in a red warning.

Note, though, that a yellow warning doesn’t necessarily escalate into a red warning when incorporated into a for-loop. The third tab demonstrates a situation where the compiler can still manage the instability effectively, even under repeated execution. This highlights that type instabilities vary in severity, and not all of them pose a meaningful threat to performance.

For-Loops and Yellow Warnings
When running for-loops, Julia will always emit a yellow warning, even if the operation is type stable. The warning can safely be disregarded, as it simply reflects the inherent behavior of iterators: they return either the next element to iterate over or nothing (a value with type Nothing) when the sequence is exhausted.

function foo()
    for i in 1:100
        i
    end
end
Output in REPL
julia>
@code_warntype foo()