pic
Personal
Website

7c. Benchmarking Execution Time

Martin Alfaro
PhD in Economics

Introduction

This section presents standard tools for benchmarking code. Our website in particular will provide results based on the package BenchmarkTools, which is currently the most mature and reliable option. Nonetheless, the newer Chairmarks package has shown impressive speed gains. Once it's been around enough to uncover potential bugs, I'd recommend it as the default option.

Time Metrics

Regardless of the package employed, Julia uses the same time metrics described below. These metrics can be accessed at any time in the left bar, under "Notation & Hotkeys".

Unit Acronym Measure in Seconds
Seconds s 1
Milliseconds ms \(10^{-3}\)
Microseconds μs \(10^{-6}\)
Nanoseconds ns \(10^{-9}\)

All packages additionally provide information about memory allocations on the heap, which are simply referred to as allocations. Their relevance will be explained in the upcoming sections. Basically, they influence performance and potentially hint suboptimal coding.

"Time to First Plot"

The expression "Time to First Plot" refers to a side effect of how the Julia language works: in each session, the first function call is slower than the subsequent ones. This arises because Julia compiles code during its initial run, as we'll explain more thoroughly in the next sections.

This overhead isn't a major hindrance when working on a large project, since the penalty will be incurred only once. However, it determines that Julia may not be the best option when you simply aim to perform a rapid analysis (e.g., run one regression or draw a graph to quickly unveil a relation).

The speed of the first run varies significantly. While it may be imperceptible in some cases, it can be noticeable in others. For instance, I bet you didn't notice that running sum(x) for the first time in your code was slower than the subsequent runs! On the contrary, drawing high-quality plots can take up to 15 seconds, explaining where the term "Time to First Plot" comes from. [note] The time indicated is for Plots, the standard package for the task. This is a metapackage bundling several plotting libraries. Some of these libraries are relatively fast, requiring less than 5 seconds for rendering the first figure.

Warning!
The time-to-first-plot issue has been reduced significantly since Julia 1.9, and each new version is reducing this overhead even further.

@time

Julia comes with a built-in macro called @time to measure the execution time of a single run. The results provided by this macro, nonetheless, suffer from two significant limitations. First, the timing provided is volatile and unreliable, as it only considers a single execution. Furthermore, considering the time-to-first-plot issue, the initial timing will incorporate compilation time, and hence it's unrepresentative of the subsequent calls. Taking this into account, you should always execute @time at least twice. The following illustrates its use, making it clear that the first run includes compilation time.

@time 
x = 1:100

@time sum(x)         # first run                     -> it incorporates compilation time 
@time sum(x)         # time without compilation time -> relevant for each subsequent run
Output in REPL 
  0.003763 seconds (2.37 k allocations: 145.109 KiB, 99.11% compilation time)
  0.000005 seconds (1 allocation: 16 bytes)

Package "BenchmarkTools"

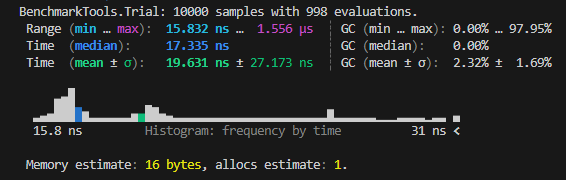
A better option for measuring execution time is provided by the package BenchmarkTools. This reports times based on repeated computations of the operation, thus improving accuracy.

It can be called through either the macro @btime, which only reports the minimum time, or through the macro @benchmark, which provides a more detailed analysis. Both macros discard the time of the first call, thus excluding compilation time from the results.

using BenchmarkTools

x = 1:100
@btime sum($x)        # provides minimum time only
Output in REPL 
  1.500 ns (0 allocations: 0 bytes)

using BenchmarkTools

x = 1:100
@benchmark sum($x)    # provides more statistics than `@btime`
Output in REPL

Notice that both macros append the symbol $ to the variable x. The notation is necessary to indicate that x shouldn't be interpreted as a global variable, as occurs when when a variable is passed to a function. As we'll exclusively benchmark functions, you should always add $ to each variable—omitting $ would lead to inaccurate results.

The following example demonstrates the consequence of excluding $, wrongly reporting higher times than they really are. [note] In fact, sum(x) doesn't allocate memory, unlike what's reported without $. 

using BenchmarkTools
x = rand(100)

@btime sum(x)
Output in REPL 
  16.132 ns (1 allocation: 16 bytes)

using BenchmarkTools
x = rand(100)

@btime sum($x)
Output in REPL 
  6.600 ns (0 allocations: 0 bytes)

Package "Chairmarks"

A recent new alternative to benchmarking code is given by the package Chairmarks. Its notation is quite similar to BenchmarkTools, with the macros @b and @be providing a similar functionality to @btime and @benchmark respectively. However, Chairmarks is orders of magnitude faster. 

using Chairmarks
x = rand(100)

display(@b sum($x))        # provides minimum time only
Output in REPL 
6.704 ns
using Chairmarks
x = rand(100)

display(@be sum($x))       # analogous to `@benchmark` in BenchmarkTools
Output in REPL 
Benchmark: 3638 samples with 3720 evaluations
min    6.694 ns
median 6.855 ns
mean   6.990 ns
max    34.462 ns

Remark On Random Numbers Used On The Website

In the upcoming sections, we'll identify efficient approaches for computing an operation. The tests will be executed relying on random numbers. To eliminate any possible bias, all of them will be based on the same random numbers, which is achieved by specifying a random seed. By doing so, the random number generator produces the same sequence of random numbers every time we execute the program.

The creation of random numbers is given by the package Random, which requires specifying a seed. You can use any arbitrary number for setting the seed, and ensure that the same seed is established before executing each operation.

using Random

Random.seed!(1234)      # 1234 is an arbitrary number, use any number you want
x = rand(100)

Random.seed!(1234)
y = rand(100)           # identical to `x`
using Random

Random.seed!(1234)      # 1234 is an arbitrary number, use any number you want
x = rand(100)


y = rand(100)           # different from `x`

When any code snippet on this website includes random numbers, we'll exclude the lines setting the random seed. For instance, below we demonstrate what we'll show versus the actual code executed.

using Random
Random.seed!(123)

x = rand(100)

y = sum(x)
# We omit the lines that seet the seed


x = rand(100)

y = sum(x)

Benchmarks In Perspective

In the upcoming chapters, we'll be evaluating approaches for performing a task. Most of the time, the differences in time will be negligible, possibly in the ballpark of nanoseconds. This could mislead us into thinking that the method chosen lacks any practical implication.

It's true that operations in isolation usually have an insignificant impact on runtime. However, the relevance of our benchmarks lies in scenarios where these operations are performed repeatedly. This includes cases where the operation is called in a for-loop, or in iterative procedures (e.g,. solving systems of equations or the maximization of a function). In these situations, small differences in timing are amplified, as they're replicated multiple times.

An Example

Let's illustrate the practical usage of benchmarks by considering a concrete case. Suppose we seek to double each element of x and then sum them. We'll compare two approaches for this task.

The first method will be based on sum(2 .* x), where x will enter into the computation as a global variable. As we'll discuss in later sections, this approach is relatively inefficient. A more efficient alternative is given by sum(a -> 2 * a, x), with x passed as a function's argument. Aside what this function specifically does, what matters is that it produces the same result as the baseline approach, but implementing a different technique.

The runtime of each approach is as follows.

x      = rand(100_000)

foo()  = sum(2 .* x)
Output in REPL 
  65.900 μs (4 allocations: 781.34 KiB)

x      = rand(100_000)

foo(x) = sum(a -> 2 * a, x)
Output in REPL 
  6.060 μs (0 allocations: 0 bytes)

The results reveal that the most efficient approach achieves a significant speedup, taking less than 15% of the slowest approach's time. However, in absolute terms, the "slow" approach is already fast enough, taking less than 0.0001 seconds.

Most of our benchmarks will feature a similar pattern, where absolute times are negligible. In this context, the relevance of the conclusions hinge on the characteristics of our work. If the operation will be called once in isolation, you should prioritize readability and choose the approach most suitable in this regard. On the contrary, if the operation will be performed repeatedly, you should consider that small differences will compound and become significant.

To demonstrate this point, let's call these functions in a for-loop with 100k iterations.

x      = rand(100_000)
foo()  = sum(2 .* x)

function replicate()
   for _ in 1:100_000
      foo()
   end
end
Output in REPL 
  22.221 s (400000 allocations: 74.51 GiB)

x      = rand(100_000)
foo(x) = sum(a -> 2 * a, x)

function replicate(x)
   for _ in 1:100_000
      foo(x)
   end
end
Output in REPL 
  650.441 ms (0 allocations: 0 bytes)

The symbol _ is a programming convention to denote "throwaway" variables. They represent variables solely included to satisfy the syntax of an operation, and their value isn't actually used. In our case, it reflects that each iteration is performing the same operation for benchmark purposes.

The example starkly reveals the consequences of calling the function within a for-loop. The execution time of the slow version balloons to more than 20 seconds now, while the fast version does it in under one second. Overall, this unveils the relevance of optimizing functions with repeated or intensive operations, where even slight improvements can have a substantial impact on performance.